Spela schack |
Om dataschack |
Koda spelbräda |
Öppningsspel |
Evalueringsfunktion |
Draggenerator |
Minimax & Alfabeta-reducering |
Dragsortering |
Slutspel |
Schackregler |
Javascript |
Länkar/referenser
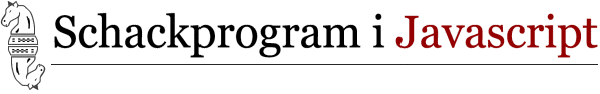
Evalueringsfunktion
Evalueringsfunktion - varför?
Evalueringsfunktionen är den som får minmax -algoritmen att jobba logiskt. På så vis kan vi flytta pjäser och testa kombinationer och studera resultatet. Får vi mer eller mindre poäng om vi gör si eller så? En evalueringsfunktion måste ge en någorlunda rättvis bild av spelet. I schack är detta möjligt därför att matrialet är så dominerande för ställningen. I andra strategispel är det svårare att göra en bra evalueringsfunktion och då blir det också svårare att göra en fungerande sökning. Om det enda man har att söka på är
vinst så blir sökningen oftast så omfattande att den direkt är omöjligt.
Vad är en pjäs värd?
Hur mycket är pjäserna värda i förhållande till varandra? Det finns lite olika förslag. Här nedan är några av dem.
|  |  |  |  |  |
| Standard 1:3:3:5:9 | 1 | 3 | 3 | 5 | 9 |
| Bobby Fischer | 1 | 3 | 3.25 | 5 | 9 |
| Sarratt, 1813 | 2/3.75 | 9.25 | 9.75 | 15 | 23.75 |
| Howard Staunton/Philidor (1817) | 1 | 3 | 3.5 | 5.5 | 10 |
| Bilguer | 1.5 | 5.3 | 5.3 | 8.6 | 15.5 |
| Yevgeny Gik | 1 | 2.4 | 4 | 6.4 | 10.4 |
| Larry Evans | 1 | 3.5 | 3.75 | 5 | 10 |
| Max Euwe/Hans Kramer | 1 | 3.5 | 3.5 | 5.5 | 10 |
| Larry Evans | 1 | 3.5 | 3.75 | 5 | 10 |
| Larry Kaufman | 1 | 3.25 | 3.25 | 5 | 9.75 |
Källa [wikipedia om pjäsernas värden]
De flesta föreslår dynamiska värden som förändras under spelet, t.ex. att bondens värde ökar mot slutet av spelet eller att löparen är värd mer om man har kvar båda.
Enbart materiellt värde
En enkel och mycket snabb evalueringsfunktion är att enbart räkna material. Pjäserna tilldelas olika
vikter eller
poäng enligt ovan och därefter skapar man en summa på så vis att man tar antalet pjäser av respektive art och multiplicerar med vikten. Man gör då också så att vita pjäser räknas positivt och svarta negativt.
E=
VB*100+VK*300+VB*450+VR*500+VQ*1000+VK*9999 -
SB*100-SK*300-SB*450-SR*500-SQ*1000-SK*9999
Vi kan notera att denna evalueringsfunktion är symetrisk och linjär. Denna evalueringsfunktion går också att optimera ganska mycket. Vi behöver t.ex. inte räkna om
denna ekvation varje gång vi undrar vad evalueringsvärdet är. Det räcker att vi håller koll på
förändringarna av värdet. Eftersom förändringar enbart äger rum när en pjäs knockas ut från bordet behöver vi bara förändra värdet med den pjäs som försvann. Vi får en enkel differensmaskin. Säg att evalueringsfunktionens värde är E. Om vi slår ut ett svart torn då behöver vi bara göra följande kalkyl för att få E.
E=E-500
Sen har vi vårt nya E som minskat med 500. Nästa gång värdet av E förändras är nästa gång en pjäs knockas ut från spelplanen.
Evalueringsfunktionens värde, E, räknas här ur vit spelares perspektiv. Lägg märke till att värdet förändras när du antingen flyttar fram pjäserna eller, i synnerhet, när du slår ut motspelarens pjäser. Om E är positivt så betyder det att vit spelare ligger över och om E är negativt så ligger E under.
Du kan prova olika evalueringsfunktioner genom att kryssa i materiellt eller komplext till höger om schackbrädan överst på sidan.
Jag använder nedanstående värden på pjäserna i detta exempel. Spelpjäsernas värden är i allt väsentligt inspirerad av ett genomsnitt av det man kan hitta i schacklitteratur. Jag har dock minskat värdet på löparen något eftersom jag aldrig riktigt förstått den pjäsen. Rent matematiskt kan den heller inte flytta till lika många positioner som t.ex. tornet. Dessa värden kan komma att ändras senare om jag kommer till andra insikter. Det kommer gå att laborera med när programmet är färdigt.
Kodexempel för en materiell evalueringsfunktion hittar du här nedan. Jag har placerat alla värden i en array. Vi kör sedan en loop över alla spelpositioner och summerar alla pjäsernas värden. Vid start skall denna summa bli noll eftersom vit's värde är lika positiva som svart's värde är negativa.
var pieceMaterial=new Array(0, 100, 500, 300, 450, 1000, 9999,0,0,0,
0,-100,-500,-300,-450,-1000,-9999,0,0,0)
function evalb(m)
{
var e=0;
for(i=0;i<64;i++)
{
e+=pieceMaterial[chessBoard[i]];
}
return e;
}
Som jag nämde under
algoritmer är denna evalueringsfunktion möjlig att optimera då värdet enbart kan förändras när en pjäs flyttas och då enbart med värdet av högst en pjäs.
Bonus för center -kontrol
Vanligt är att man brukar premiera pjäser som placerar sig i mitten av spelplan. Jag skapar en matris jag kallar
areaCtrl som jag initierar med lite värden på spelplanens mitt.
var areaCtrl = new Array( 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 0, 0,
0, 0, 1, 2, 2, 1, 0, 0,
0, 0, 1, 2, 2, 1, 0, 0,
0, 0, 1, 1, 1, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0);
Därefter skriver jag en ny evalueringsfunktion som lägger till dessa värden ifall det står en spelpjäs på dessa positioner. Jag lägger till bonusvärdet om pjäsen är vit och drar ifrån det om pjäsen är svart. Jag använder värdet på pjäsen (p) för att avgöra färgen (vit är 1-6 och svart är 11-16).
function evalc(m)
{
var e=0,p;
for(i=0;i<64;i++)
{
p=chessBoard[i];
e+=pieceMaterial[p];
if ((p>0)&&(p<8)) // vit pjäs
{
e+=areaCtrl[i];
}
if (p>8) // svart pjäs
{
e-=areaCtrl[i];
}
}
return e;
}
Komplex evaluering
I det optimala fallet skall en evalueringsfunktion ta hänsyn till allt sådant människor tar hänsyn till, vilket inkluderar t.ex.
Material (pjäser)
Rörlighet
Kungens trygghet
Kontroll på mittplan
Strukturen på böndernas placering
Hotade pjäser
osv.
Vi tänker oss en evalueringsfunktion som ser ut så här, där K är en vikt och F det som ska beaktas.
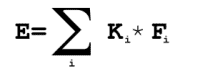
Ekvationen blir genast mycket mer komplex och abstrakt. Vi kan ju räkna på allt - men är det intressant? Vi måste formulera en
heuristik för det vi vill göra.
Material + Lite Komplex
Vi kan också följa en medelväg. Säg att vi räknar material och tar de delar som är enkla att räkna ut från en komplex evaluering. Ett program som följer denna metod är t.ex. GNU-Chess.
Hur avancerad skall en evalueringsfunktion vara? Det finns 2 olika skolor i detta ämne. Den ena förespråkar en enkel evalueringsfunktion så att man får tid till mycket sökning. Argumenten för denna metod är att det är sökningen som gör allt jobb och ju mer sökning desto bättre schackspel. Den andra förespråkar en avancerad evalueringsfunktion även till priset av att man då inte hinner söka lika mycket. Argumenten för denna metod är att trots mycket sökning klår bra schackspelare de flesta schackdatorer. Hemligheten i bra schackspel ligger enligt dessa därför omöjligt i sökprocessen utan i andra faktorer.