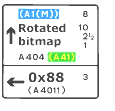
Detta är tredje versionen av spelbrädans kodning. Tydligen måste man ibland göra en del misstag för att komma till vissa insikter, men nu har jag fått ordentlig kläm på exakt hur jag ska tänka.

Siffror här nedan som är på formen 0x10 eller 0x2C är hexadecimala tal. Jag har valt denna skrivform eftersom talen här är valda för att de har vissa binära egenskaper. Det hexadecimala skrivsättet är enklare att överföra till binär form än det decimala.

Själv spelbrädan har jag nu gjort efter 0x88 som förebild. Det innebär att jag använder en matris på 16x8 rutor, detta för att placera pjäserna på positioner med vissa binära egenskaper.

var cb0x88 = new Array(
  0x12,0x13,0x14,0x16,0x15,0x14,0x13,0x12,0,0,0,0,0,0,0,0,
  0x11,0x11,0x11,0x11,0x11,0x11,0x11,0x11,0,0,0,0,0,0,0,0,
  0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0,0,0,0,0,0,0,0,
  0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0,0,0,0,0,0,0,0,
  0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0,0,0,0,0,0,0,0,
  0x00,0x00,0x00,0x00,0x00,0x00,0x00,0x00,0,0,0,0,0,0,0,0,
  0x01,0x01,0x01,0x01,0x01,0x01,0x01,0x01,0,0,0,0,0,0,0,0,
  0x02,0x03,0x04,0x06,0x05,0x04,0x03,0x02,0,0,0,0,0,0,0,0);

Ovanstående matris betyder att schackbrädan ser ut som till höger. Själva poängen med att göra detta är som jag nämde att ge spelhalvan av denna konstruktion positioner med vissa binära egenskaper. Dessa binära egenskaper gör att vi kan skilja på nummer som befinner sig på och utanför schackbrädan genom en enkel logisk bitvis jämförelse. Att vi kan göra denna enkla jämförelse betyder senare att vi kan göra en mycket snabb draggenerator.

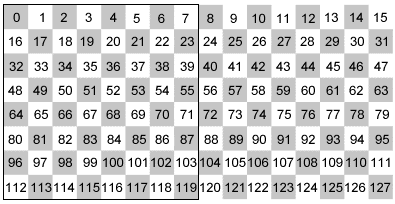
Studera siffrorna här till höger och titta sedan på den tabell med binära tal du ser nedan. Jag har klippt in binära tal för några negativa nummer samt nummer utanför schackbrädans positioner.

Titta riktigt noga på den första 1:an eller 0:an i varje gruppering.

  XYYY XYYY

Gemensamt med den inringade schackbrädan är att varje första bit i grupperingarna båda är noll. Placeringar utanför schackbrädan har det gemensamt att där är första biten i dessa grupperingar 1. Notera hur de negativa binära talen ser ut eftersom datorer använder 2-komplement. Denna systematiska skillnad kan vi enkelt identifiera genom att ta en position på eller utanför spelbrädan och göra en logisk AND med 0x88 (binärt 1000 1000).

-1	1111 1111	0	0000 0000	32	0010 0000	64	0100 0000	96	0110 0000	128	1000 0000
-2	1111 1110	1	0000 0001	33	0010 0001	65	0100 0001	97	0110 0001	129	1000 0001
-3	1111 1101	2	0000 0010	34	0010 0010	66	0100 0010	98	0110 0010	130	1000 0010
-4	1111 1100	3	0000 0011	35	0010 0011	67	0100 0011	99	0110 0011	131	1000 0011
-5	1111 1011	4	0000 0100	36	0010 0100	68	0100 0100	100	0110 0100	132	1000 0100
-6	1111 1010	5	0000 0101	37	0010 0101	69	0100 0101	101	0110 0101	133	1000 0101
-7	1111 1001	6	0000 0110	38	0010 0110	70	0100 0110	102	0110 0110	134	1000 0110
-8	1111 1000	7	0000 0111	39	0010 0111	71	0100 0111	103	0110 0111	135	1000 0111
-9	1111 0111	8	0000 1000	40	0010 1000	72	0100 1000	104	0110 1000	136	1000 1000
-10	1111 0110	9	0000 1001	41	0010 1001	73	0100 1001	105	0110 1001	137	1000 1001
-11	1111 0101	10	0000 1010	42	0010 1010	74	0100 1010	106	0110 1010	138	1000 1010
-12	1111 0100	11	0000 1011	43	0010 1011	75	0100 1011	107	0110 1011	139	1000 1011
-13	1111 0011	12	0000 1100	44	0010 1100	76	0100 1100	108	0110 1100	140	1000 1100
-14	1111 0010	13	0000 1101	45	0010 1101	77	0100 1101	109	0110 1101	141	1000 1101
-15	1111 0001	14	0000 1110	46	0010 1110	78	0100 1110	110	0110 1110	142	1000 1110
-16	1111 0000	15	0000 1111	47	0010 1111	79	0100 1111	111	0110 1111	143	1000 1111
-17	1110 1111	16	0001 0000	48	0011 0000	80	0101 0000	112	0111 0000	144	1001 0000
-18	1110 1110	17	0001 0001	49	0011 0001	81	0101 0001	113	0111 0001	145	1001 0001
-19	1110 1101	18	0001 0010	50	0011 0010	82	0101 0010	114	0111 0010	146	1001 0010
-20	1110 1100	19	0001 0011	51	0011 0011	83	0101 0011	115	0111 0011	147	1001 0011
-21	1110 1011	20	0001 0100	52	0011 0100	84	0101 0100	116	0111 0100	148	1001 0100
-22	1110 1010	21	0001 0101	53	0011 0101	85	0101 0101	117	0111 0101	149	1001 0101
-23	1110 1001	22	0001 0110	54	0011 0110	86	0101 0110	118	0111 0110	150	1001 0110
-24	1110 1000	23	0001 0111	55	0011 0111	87	0101 0111	119	0111 0111	151	1001 0111
-25	1110 0111	24	0001 1000	56	0011 1000	88	0101 1000	120	0111 1000	152	1001 1000
-26	1110 0110	25	0001 1001	57	0011 1001	89	0101 1001	121	0111 1001	153	1001 1001
-27	1110 0101	26	0001 1010	58	0011 1010	90	0101 1010	122	0111 1010	154	1001 1010
-28	1110 0100	27	0001 1011	59	0011 1011	91	0101 1011	123	0111 1011	155	1001 1011
-29	1110 0011	28	0001 1100	60	0011 1100	92	0101 1100	124	0111 1100	156	1001 1100
-30	1110 0010	29	0001 1101	61	0011 1101	93	0101 1101	125	0111 1101	157	1001 1101
-31	1110 0001	30	0001 1110	62	0011 1110	94	0101 1110	126	0111 1110	158	1001 1110
-32	1110 0000	31	0001 1111	63	0011 1111	95	0101 1111	127	0111 1111	159	1001 1111

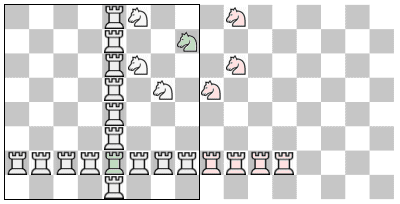
Det betyder alltså att om vi har en postition fpos, då kan vi alltså enkelt testa om denna position finns på schackbrädan med följande enkla och vackra logik. Vi filtrerar enkelt bort alla drag som inte hamnar på schackbrädan. Om du fortfarande inte kopplat varför metoden kallas 0x88 kanske börjar gå upp ett ljus nu.
Denna enkla logik kan vi arbeta vidare på. Vi kan göra en snurra som adderar eller subtraherar tal för att få alla schackdrag och vi kan enkelt utesluta det drag som hamnar utanför spelplanen.

Om man stångas ett tag med draggenereringen kan man identifiera den logik som draggeneratorn behöver för att fungera.
Inspirerad av de enkla lösningar 0x88:an ger när det gäller att testa om drag är innanför eller utanför kan vi skapa samma sköna logik för andra frågor som dyker upp i draggeneratorn.

Efter lite funderande kan man t.ex. komma fram till att följande pjäskodning är väldigt effektiv, betraktat som ett 8-bitars tal. Detaljen som gör skillnad är hur jag kodar pjäsens färg.



Jag har valt att koda pjäserna på följande sätt.


Varför dessa värde? Varför inte bara ge dem index från 1-6 för vit och t.ex. 11-16 för svart? Poängen med att koda pjäserna på det ena eller andra sättet är att vissa sätt att koda gör det möjligt att göra enkla tester på schackbrädan. Sådana tester vi vill göra inkluderar t.ex.

• Står där en vit pjäs?
• Står där en pjäs av motsatt färg?
• Står där en pjäs av motsatt färg eller är rutan tom? ¹
• Vilken pjästyp är det?
• Har pjäsen flyttat tidigare?
• Är pjäsen attackerad? (exempelvis schack)

¹ Speciellt denna fråga är intressant t.ex. när vi flyttar en glidande pjäs över schackbrädan. Säg att vi flyttar ett svart torn över spelbrädan. Villkoret för att kunna flytta tornet till en ruta är att rutan antingen är tom eller att där står en vit pjäs (som vi då slår ut). Men vi kan inte flytta utanför spelbrädan och vi kan inte köra över en pjäs av vår egen färg.

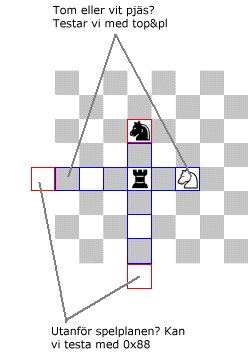
Kodningen av vad som är vitt och svart ger oss en enkel skön logik för detta. För att t.ex. testa nyss nämda ser koden ut så här ...

Det är nästan så att man undrar vart koden tagit vägen, så kompakt blir det. Tillsammans med den enkla logiken som 0x88 -brädan ger borde vi krattat manegen för en snygg kompakt och snabb kod. Läs mer om detta under draggenereringen.

N -biten använder vi för att avgöra om en pjäs har flyttats eller inte. Så fort vi flyttar en pjäs första gången sätter vi denna bit till noll. Därefter förblir den noll. Informationen används bl.a. när vi skall avgöra om rockad är legalt eller inte, då vi behöver veta om kungen eller tornen har flyttats någon gång.

Anpassa: Georgia | Verdana | Större | Mellan | Mindre | Utskriftsvänlig | Normal centrerad
©2007 - 20010 Alla Rättigheter Förbehålles