Slutspel

Allmänt

När övergår spelet i slutspel? Definitionen flyter lite beroende på vem man frågar. Vissa menar att slutspel inleds när det inte längre finns något uppenbart sätt att göra schackmatt, t.ex. när det bara finns 2 kungar och löpare kvar. Andra definierar slutspel lite vidare. Ett konkret förslag (källa: Wikipedia Endgame) är det att slutspel uppstår när poängen av antalet pjäser (kungen räknas inte) på spelplanen är 13 eller mindre räknat enl. följande.


1	3	3	5	9

Det är denna definition jag kommer använda mig av.

För minimax som lotsat fram datorn under hela matchen innebär slutspelet tilltagande problem. Det kommer behövas lite exempel och resonemang för att ta sig igenom detta. Jag delar för enkelhets skull in detta slutspel i 2 avsnitt.

Inledande slutspel. Det är teoretiskt möjligt att göra schackmatt på kanske 5 drag. En människa kan i detta läge se ungefär hur schackmatt ska göras. Denna del är ganska svår för en dator.
Avslutande slutspel. Det är möjligt att göra schackmatt på 2-3 drag. Pjäserna ska positioneras för att inkassera segern. Ett dåligt kodat schackprogram kan här orsaka stora pinsamheter.

Jag skall börja med det avslutande slutspelet och problematiken däromkring.

Ett spontant uppenbart sätt att koda slutspelet i schack är att tänka sig att det inte behövs någon speciell kodning alls. Man ger kungen maximalt med poäng och låter helt enkelt minimax hitta ett sätt att slå ut kungen. That´s it. Denna slutsats bevisar att du förstått hur minimax fungerar.

Det kan gå bra. Men det kan också gå väldigt dåligt. Datorn kan börja göra irrationella pinsamma drag. En skickligt spelad match av datorn där enbart några drag återstår för att göra schackmatt kan istället resultera i en dåraktig avslutning där programmet förlorar. Här kommer lite exempel på situationer som måste hanteras på något sätt av programmet.

Undvika att skapa patt/remi av misstag (1)

Studera brädan här till vänster, bild 1. Svart kalkylerar ett drag 3 ply fram. Efter lite tänkande kommer

Bild 1.

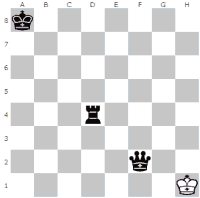
programmet fram till att om den flyttar tornet till D5 så ger detta ett alfa-värde på ca 10000, alltså schack-matt. Fast en människa ser ju direkt att det är en flytt till D1 som ger schack-matt. Är detta ett error? Minimax-algoritmen tänker så här. Jag flyttar tornet till D5. Sen är det vit på tur. Oavsett vad vit flyttar går det att slå ut kungen vilket alltså ger ett alfavärde som indikerar schackmatt.

Varför just till D5 kan man undra? Jo, D5 råkar ligga före andra drag i listan av drag som testas och när minimax hittat ett alfavärde på ca 10000 så överträffas inte det av något annat.

Vad gör programmet för fel? Jo schack-matt handlar inte om att slå ut kungen någon gång där framme utan mer explicit om att sätta kungen i schack på ett sådant sätt att kungen inte kan flytta.

Bild 2.

Ponera att vi introducerar ytterligare en vit pjäs, bonde på G6. Då kan vit göra ett alternativt drag till att flytta kungen, vit kan t.ex. flytta bonden. Då räknar datorn snabbt fram till att den måste flytta tornet till H4 för att göra schack-matt, vilket förefaller korrekt. Det är antagligen vad en människa också skulle gjort.

Så lite fler pjäser på spelplanen så kanske detta problem aldrig uppstår?

Men titta på spelplanen (nr 3) till höger här. Nu har vit placerat bonden på G5 (istället för G4). Programmet gör nu åter ett korkat drag där den påstår att de mest optimala är att flytta tornet till G4.

Draget till G4 ger ett alfavärde på ca 10000, vilket säger att datorn kan slå ut kungen nästa drag - alltså schackmatt. Vit kan inte flytta bonden och måste flytta kungen, vilket gör att datorn nästa drag kan slå ut kungen. Detta är rent logiskt korrekt men inte vad vi önskar. Nu är det ju remi.

Bild 3.

Varför gör programmet detta drag? Draget råkar ligga före andra drag i draggeneratorns lista. När minimax hittar detta drag, som ju ger schackmatt enligt alfavärdet, så nöjer den sig med detta då värdet inte överträffas av något annat. Samma problem som bild 1.

Vi måste hitta en mer offensiv lösning lösning på ofrivillig remi. En lösning är att introducera en asymetrisk dummy-regel som gäller utmanarens kung; där kungen tillåts att stå stilla. Om detta är ett legalt drag så blir inte längre alfavärdet 10000 i ovanstående situationer. Datorn måste då attackera för att slå ut kungen och få ett högt alfavärde.

Hittar schackmatt - men kommer aldrig till handling (2)

Detta problem är besläktat med föregående problem. Algoritmen minimax har inget djupseende. Den returnerar det bästa draget givet min och maxreglerna. Om draget ger resultat direkt eller 4 ply fram ser inte algoritmen.

Bild 4.

Studera bild 4. Programmet är inställt att söka på 4 ply fram. Efter en stunds tänkande kommer programmet fram till att den kan skapa schackmatt genom att flytta tornet från A8 till B8. Minimax returnerar ett alfavärde på ca 10000 så det är inget error. Vad är problemet denna gång?

Problemet är att programmet har hittat schackmatt, men inte det snabbaste schackmatt! Antagligen har minimax kommit fram till att den först skall flytta till B8 och därefter flytta tornet till B1 som ger schackmatt. Även i detta fall råkar draget A8 - B8 ligga överst bland dragen programmet undersöker och när den hittat schackmatt är det inget som överträffar detta. Om vi för skoj skull sänker sökdjupet från 4 ply till 3 ply och gör samma sökning då hittar datorn ganska snabbt det mest optimala draget, nämligen från A8 till A1 som ger schackmatt.

Hur kan vi introducera ett djupseende i algoritmen så att ifall det finns en schackmatt 2 ply fram så skall den inte hålla på att tramsa sig utan gå direkt till handling.

En lösning på detta problem är att lägga in lite mer kod i den iterativa fördjupningen av sökningen.

function IDNegaMaxAlfaBeta(maxdepth,maxtime)
{
	timestart=timer();
	for (depth=1;depth<=maxdepth;depth++)
	{
		NegaMaxAlphaBeta(depth, -999999, 999999);
		timenow=timer();

		if (maxAlpha>whiteKingAlfa)
		{
			Vit säger schack
			break;
		}

		if (maxAlpha<blackKingAlfa)
		{
			Svart säger schack
			break;
		}


		if (avbryt || ((timenow-timestart)>maxtime))
			break;
	}
}

Metoden förutsätter att vi varje gång vi kör ett varv med NegaMaxAlfaBeta fångar upp maxAlpha. Det kan vi göra samtidigt som vi fångar upp draget.

Speciell kod för att hantera schack/schackmatt

För att få en vettig lösning på hanteringen av schack måste man sätta sig ner med ett blankt papper på ritbordet och börja från början. Följande måste hanteras

Schack
Schackmatt
Patt

Schack innebär att kungen hotas. Vi måste då antingen flytta kungen till en ohotad position eller göra ett drag med en annan pjäs som eliminerar själva hotet; dvs antingen ställa oss mellan pjäsen som hotar och kungen eller slå ut pjäsen som hotar.

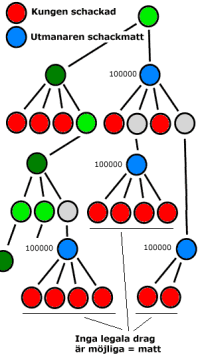
Schackmatt innebär att vi misslyckats med ovanstående. Det finns inget drag som kan göras som eliminerar hotet. Spelet är slut.

Vad man kan ta fasta på är att om vi blir schackade så måste vi hantera situationen omedelbart. Det är alltså helt poänglöst att söka vidare på olika kombinationer om vi blir av med kungen. Alla drag som inte hanterar schack:et är ointressanta därför att det är drag som leder till att vi förlorar. Det strider dessutom mot schackreglerna att inte flytta en hotad kung ifall det finns en möjlighet.

Det smartaste verkar helt enkelt vara att förändra hur minimaxalgoritmen arbetar i en situation då en kung är schackad. Vi testar om vi befinner oss i en schack-nod och om så är fallet försöker vi ta oss ur schack-situationen. Samtidigt räknar vi antalet vägar ur schack-situationen. Om denna siffra är, eller snarare förblir, noll, så har vi ett schack-matt. Dessutom - eller oavsett vilket - så söker vi inte heller djupare i trädet i en schack-situation då det är bortkastad tid. Detta tillsammans med en liten bonus för schack som ligger närmare roten i trädet åtgärdar problem (2) beskrivet ovan med att programmet hittar schackmatt men kommer aldrig till handling.

Det uppstår här också ett bra sätt att hantera patt på vilket åtgärdar problemet (1) med ofrivillig patt. Läs lite längre ner om detta.

Ytterligare fördel med denna teknik är att vi upptäcker schackmatt 1 ply snabbare än alternativet med att implicit (indirekt) låta minimax slå ut kungen för att identifiera ett schack/schackmatt. Om du tittar på t.ex. bild 4 här ovan så ser du att det krävs 3 ply för att identifiera schackmatt om minimax skall slå ut kungen för att hitta schackmatt. Med separat kod som kontrollerar om kungen står i schack behövs bara 2 ply för att identifiera schackmatt.

Följande är ett förslag på pseudokod för hur minimaxalgoritmen bör konstrueras. Studera hur jag gjort på raderna 17 - 40 samt raderna 9 - 10.

 1 function NegaMax(var depth, var tp)
 2 {
 3    if (depth == 0)
 4    {
 5       return Eval();
 6    }
 7    Skapa en lista av alla drag
 8 
 9    bcheck=schackad();
10    lMoves=0;
11 
12    best = -99999999;
13    while (drag kvar att göra)
14    {
15       Gör ett drag i listan
16 
17       if (check=schackad())
18       {
19          while (check && (drag kvar att göra))
20          {
21             Ta tillbaka draget
22             Gör ett drag i listan
23             check=schackad()
24          }
25          if ((INGA drag kvar att göra)&&(lMoves==0))
26          {
27             Ta tillbaka draget
28             if (bcheck)
29             {
30                E = -100000-depth;
31             }
32             else
33             {
34                E = -pattVal;
35             }
36             return E;
37          }
38          check=false;
39       }
40       lMoves++;
41 
42       temp=-Negamax(depth-1,1-tp)   
43       Ta tillbaka draget
44       if (temp>best)
45       {
46          best=temp;
47       }
48    }
49    return best;
50 }

Raderna 19-24: Om vårt drag ur draggeneratorns lista lämnar oss kvar i schack är det ett illegalt drag och vi tar därför tillbaka draget och provar ett nytt. Vi provar dragen ett i taget tills vi hittar ett legalt drag som tar oss ur schack.

De situationer som kan inträffa är att antingen finns ett drag som tar oss ur schack eller så finns inget drag, detta mäter räknaren lMoves. Om det finns minst ett drag så kan vi alltså göra detta drag. Finns inget drag som tar oss ur schack så innebär det att partiet är förlorat. Vi kan då t.ex. returnera 100.000 som jag gjort här eller returnera ett värde för patt (se nedan under rubriken "patt"). För att veta om det är schackmatt eller patt tittar vi på situationen innan vi försökta göra några drag. Variabeln bcheck innehåller värdet på om vi var schackade eller inte innan vi gjorde något drag.

Rad 30 är viktig, där jag lägger till värdet av depth till det höga returvärdet. Genom att öka returvärdet något vid grundare djup bör vi uppnå effekten att datorn föredrar ett schackmatt som går att göra i närtid. Detta löser problemet beskrivet ovan med att minimax kan hitta schackmatt men aldrig komma till handling.

För att tekniken ovan ska fungera krävs som nämts en funktion som testar om kungen befinner sig i schack. Denna har fått följande utseende.

function isChecked(pl,kpos)
{
   var t,jx, ix, ox;
   jx=13; //  13, där ligger först torn + 0 + löpare
   ctm[kpos]=0;
   pla=(pl?0x10:0x20);
   while (t=moff[jx++]) // torn | drottning 's rörelser
   {
      ix=0;
      while(++ix<9)
      {
         ox=kpos+ix*t;
         if (ox&0x88) break;
         if ((cb[ox]&(0x04|pla))==(0x04|pla))
         {
            return true;
         }
         if (cb[ox]&0x3F) break;
      }
   }
   while (t=moff[jx++]) // löpare | drottning's rörelser
   {
      ix=0;
      while(++ix<9)
      {
         ox=kpos+ix*t;
         if (ox&0x88) break;
         if ((cb[ox]&(0x08|pla))==(0x08|pla))
         {
            return true;
         }
         if (cb[ox]&0x3F) break;
      }
   }
   jx=32; // häst
   while (t=moff[jx++]) // häst
   {
      ox=kpos+t;
      if (!(ox&0x88))
      {
         if ((cb[ox]&(0x0F|pla))==(0x02|pla))
         {
            return true;
         }
      }
   }
   while (t=moff[jx++]) // kung
   {
      ox=kpos+t;
      if (!(ox&0x88))
      {
         if ((cb[ox]&(0x03|pla))==(0x03|pla))
         {
            return true;
         }
      }
   }
   jx=0; // bonde för pm
   while (t=pm[jx++]) // bonde
   {
      ox=kpos+(pl?t:-t); // pl=0 då -t annars +t
      if (!(ox&0x88))
      {
         if ((cb[ox]&(0x01|pla))==(0x01|pla))
         {
            return true;
         }
      }
   }
   return false;
}

Vad jag gör är helt enkelt att utgå ifrån kungens position. Dvs, jag söker schackbrädan horisontellt och vertikalt och testar om det står ett torn eller drottning på någon av dessa positioner. Jag testar diagonalt efter en löpare eller drottning. Jag testar hästens positioner om där står en häst. Funktionen returnerar sant så fort den hittat en pjäs som hotar kungen annars returnerar den falskt.

Patt

Patt innebär att ingen vinner - det är oavgjort. Hur skall detta hanteras? Spontant kan man ju tycka att patt är helt värdelöst och bör få noll poäng. Men ponera en match där datorn ligger hopplöst under. Datorn har förlorat massor av viktiga pjäser och det är bara en tidsfråga innan datorn förlorar. Om datorn i en sådan situation hittar patt - är det då inte ganska smart av datorn att hellre få matchen att bli oavgjort än att förlora matchen? Naturligtvis är det bättre med en oavgjort match i ett sånt läge! Omvänt - om vi har ett övertag då vill vi naturligtvis inte ha oavgjort. Utmanarens försök att skapa oavgjort skall motarbetas. I en sådan situation; om datorn kan vinna matchen vore det oerhört pinsamt om datorn skapade oavgjort.

Om man köper detta resonemang så vill vi alltså skapa ett flexibelt värde på patt. Har vi ett underläge skall patt betraktas som något bra. Har vi ett överläge skall patt betraktas som något dåligt. Hur vet vi om vi ligger över eller under? Tja, vi kan väl räkna pjäserna som evalueringsfunktionen gör och låta det materiella övertaget/underläget avgöra matchens läge.

Studera raderna 28 - 35 här ovan. Ponera att det är vår tur att göra ett drag. Om motspelare har satt oss i schack då måste vi hantera detta schack. Kan vi inte ta oss ur schacket har vi förlorat. För att veta om vi är schackade testar jag detta på rad 9 och sätter variabeln bcheck. Om bcheck är sann och vi inte kan ta oss ur schack är det alltså schackmatt. Men om bcheck är falskt, vi är alltså inte schackade, och alla drag vi kan göra försätter oss i schack - då är det inte schackmatt utan patt (oavgjort).

Patt -problematiken är intimt besläktigad följande problem:

Remi genom 3 samma drag

En schackregel säger att om ett drag upprepas 3 gånger så kan en spelare begära remi, dvs i praktiken är det remi (oavgjort).

Detta är ännu ett lurigt problem att hantera. Om vi inte hanterar detta på något sätt kan det mycket väl inträffa att datorn trampar i denna fälla.

Men vad ska vi göra? Skall vi konsekvent undvika att göra remi genom 3 samma drag? Ovanstående patt -resonemang är helt kompatibelt med detta problem. Det är ungefär samma strategiska logik fast med en liten viktig skillnad. Pattsituationen inträffar i slutet av spelet medans dragupprepning kan inträffa var som helst i spelet. Om vi befinner oss i mitten av spelet eller i början av spelet är det långt ifrån givet vem som vinner. Skall vi fatta beslutet att orsaka medveten remi genom dragupprepning måste vi ligga ordentligt under. Dvs, det måste vara utom allt rimligt tvivel att vi kommer förlora.

Vi kan alltså använda samma beslutslogik som för pattsituationen men vi ökar kravet på att vi ligger under för att acceptera remi på detta sätt. Om vi inte ligger ordentligt under så skall remi genom dragupprepning bestraffas poängmässigt.

Max 50 drag -regeln

Ytterligare ett närbesläktat problem är regeln som säger att en match inte får vara längre än 50 drag. Skall vi fortsätta med ovanstående resonemang kan vi alltså tänka oss att ifall vi ligger hopplöst under så genom att hålla oss flytande under 50 drag så har vi skapat oavgjort. Eller något sånt. Problemet här är följande: Vi kan inte söka så långt fram att vi kan använda denna information på något vettigt sätt. Betraktat ur minimax perspektiv är detta slut som en blixt från klar himmel. Plötsligt är det bara 4 halvdrag kvar. Det kommer inte gå att göra något som jag kan överblicka just nu. Har du någon briljant ide' på detta problem hör av dig!

Tänkbara sätt att få in denna parameter i programmet är att t.ex. antalet drag är en variabel i den dynamiska Patt -funktionen som jag beskrivit ovan. Om vi t.ex. har spelat 40 drag så även om antal pjäser på spelplanen är många så kan vi öka belöningen för att orsaka oavgjort. Å andra sidan har det gått 40 drag och många pjäser finns kvar så existerar i praktiken aldrig möjligheten för remi.

Inledande slutspel

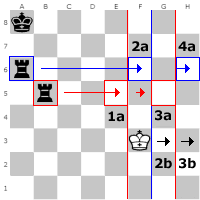
Den fas i slutspelet som handlar om att leda spelet mot schackmatt rent strategiskt kallar jag inledande slutspel. Kännetecknande för detta läge i spelet är att man som människa kan se hur ett schackmatt kan gestalta sig, men det är för långt bort för att datorn skall hitta det genom ren sökning (avslutande slutspel).

Om man tar bilden till höger som exempel. Här förstår man ju att spelet är över. Vad det handlar om är att tränga in kungen i högerfilen ömsom med tornen så har vi vunnit spelet. Men att få datorn att känna igen dessa och liknande situationer är en hel vetenskap. Just detta exempel kan en snabb dator klura ut med ren råstyrka om den har ett tillräckligt högt sökdjup, ca 8 ply. Men oftast har man inte denna styrka och definitivt inte med javascript. Här kommer vi få katastofala horisontproblem och sannolikt kommer programmet irra omkring som idiot med tornen och kanske på sin höjd göra ett ogenomtänkt schack. Har vi tur så hittar datorn schackmatt. Men tur har man sällan när man behöver det. Läs på om Murphys lag.

Vad vi måste göra är att hitta på något tillägg till evalueringsfunktionen så att minimax begriper i vilken riktning den ska arbeta i dessa situationer.